Compléments SQL

Une géométrie non valide est la cause principale de l'échec des requêtes spatiales.

Dans 90% des cas la réponse à la question “pourquoi mes requêtes me renvoient un message d'erreur du type 'TopologyException error' est : “un ou plusieurs des arguments passés sont invalides”. Ce qui nous conduit à nous demander : que signifie invalide et pourquoi est-ce important ?

La validité est surtout importante pour les polygones, qui définissent des surfaces et requièrent une bonne structuration.

Certaines des règles de validation des polygones semblent évidentes, et d'autres semblent arbitraires (et le sont vraiment) :

• Les contours des polygones doivent être fermés.

• Les contours qui définissent des trous doivent être inclus dans la zone définie par le contour extérieur.

• Les contours ne doivent pas s'intersecter (ils ne doivent ni se croiser ni se toucher).

• Les contours ne doivent pas toucher les autres contours, sauf en un point unique.

Les deux dernières règles font partie de la catégorie arbitraire.

PostGIS est conforme au standard OGC OpenGIS Specifications.

Les entités géométriques des bases PostGIS doivent ainsi être à la fois simples et valides.

Par exemple, calculer la surface d'un polygone comportant un trou à l'extérieur ou construire un polygone à partir d'une limite non simple n'a pas de sens.

Selon les spécifications de l'OGC, une géométrie simple est une géométrie qui ne comporte pas de points géométriques anormaux, comme des auto-intersections ou des auto-tangences, ce qui concerne essentiellement les points, les multi-points, les polylignes et les multi-polylignes.

La notion de géométrie valide concerne principalement les polygones et les multi-polygones et le standard définit les caractéristiques d'un polygone valide.

Un point est par nature simple, ayant une dimension égale à 0.

Un objet multi-points est simple si tous les points le composant sont distincts.

Une polyligne est simple si elle ne se recroise pas (les extrémités peuvent être confondues, auquel cas c'est un anneau et la polyligne est close).

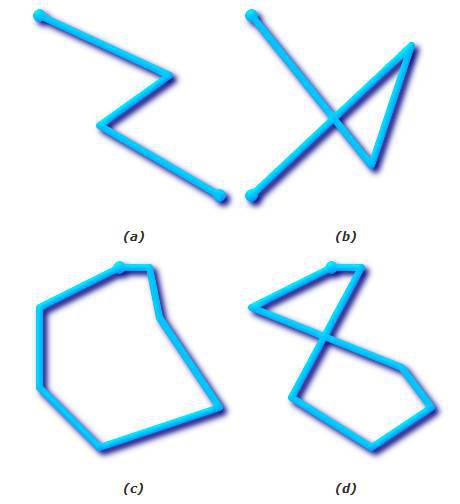
Une multi-polyligne est simple si toutes les polylignes la composant sont elles-mêmes simples et si les intersections existant entre 2 polylignes se situent à une extrémité de ces éléments :

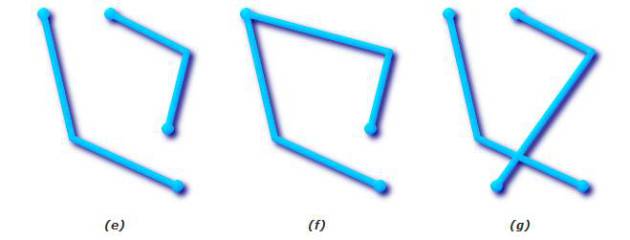
Un polygone est valide si ses limites, qui peuvent être constituées par un unique anneau extérieur (polygone plein) ou par un anneau extérieur et un ou plusieurs anneaux intérieurs (polygone à trous), ne comporte pas d'anneaux se croisant.

Un anneau peut intersecter la limite mais seulement en un point (pas le long d'un segment).

Un polygone ne doit pas comporter de lignes interrompues (les limites doivent être continues) ou de point de rebroussement (pic).

Les anneaux intérieurs doivent être entièrement contenus dans la limite extérieure du polygone.

Un multi-polygone est valide si et seulement si tous les polygones le composant sont valides et si aucun intérieur d'un polygone ne croise celui d'un autre.

Les limites de 2 polygones peuvent se toucher, mais seulement par un nombre fini de points (pas par une ligne).

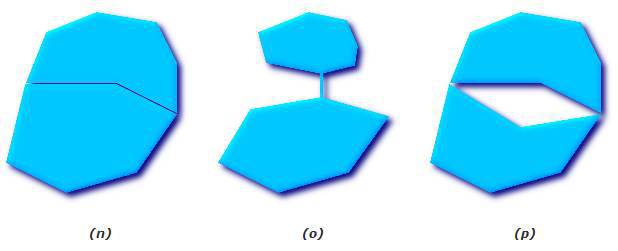
Par défaut, PostGIS n'applique pas le test de validité géométrique lors de l'import d'entités géométriques, parce que le test de validité géométrique consomme beaucoup de temps processeur pour les géométries complexes, notamment les polygones.

Il faut donc mettre en œuvre différentes méthodes pour vérifier la validité de la géométrie des entités.

Exemple :

Le polygone POLYGON((0 0, 0 1, 2 1, 2 2, 1 2, 1 0, 0 0)) n'est pas valide

Le contour externe est exactement en forme en 8 avec une intersection au milieu.

Notez que la fonction de rendu graphique est tout de même capable d'en afficher l'intérieur, donc visuellement cela ressemble bien à une “aire” : deux unités carré, donc une aire couplant ces deux unités.

Essayons maintenant de voir ce que pense la base de données de notre polygone en calculant sa surface :

SELECT ST_Area(ST_GeometryFromText('POLYGON((0 0, 0 1, 1 1, 2 1, 2 2, 1 2, 1 1, 1 0, 0 0))'));

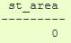
Que ce passe-t-il ici ?

L'algorithme qui calcule la surface suppose que les contours ne s'intersectent pas.

Un contour normal devra toujours avoir une surface qui est bornée (l'intérieur) dans un sens de la ligne du contour (peu importe le sens).

Cependant, dans notre figure en 8, le contour externe est à droite de la ligne pour un lobe et à gauche pour l'autre.

Cela entraîne que les surfaces qui sont calculées pour chaque lobe annulent la précédente (l'une vaut 1 et l'autre -1) donc le résultat est une surface égale à 0.

- Détecter la validité

Dans l'exemple précédent nous avions un polygone que nous savions non-valide.

Comment déterminer les géométries non valides dans une table d'un million d'enregistrements ?

Avec la fonction ST_IsValid(geometry) utilisée avec notre polygone précédent, nous obtenons rapidement la réponse :

SELECT ST_IsValid(ST_GeometryFromText('POLYGON((0 0, 0 1, 1 1, 2 1, 2 2, 1 2, 1 1, 1 0, 0 0))'));

résultat : f (false)

Maintenant nous savons que la géométrie de l'entité n'est pas valide mais nous ne savons pas pourquoi.

Nous pouvons utiliser la fonction ST_IsValidReason(geometry) pour trouver la cause de non validité :

SELECT ST_IsValidReason(ST_GeometryFromText('POLYGON((0 0, 0 1, 1 1, 2 1, 2 2, 1 2, 1 1, 1 0, 0 0))'));

résultat : Self-intersection[1 1]

En plus de la cause d'invalifdité (auto-intersection), la localisation de la non validité (coordonnée (1 1)) est aussi renvoyée.

Nous pouvons aussi utiliser la fonction ST_IsValid(geometry) pour tester les tables comme dans l'exemple suivant :

SELECT ST_IsValidReason(geom) FROM monschema.table WHERE Not ST_IsValid (geom);

Nous ébauchons ici la problématique des géométries invalides et des corrections envisageables.

Pour créer une table de géométries invalides dans le schéma travail:

exécuter le script SQL ci-dessous :

CREATE TABLE travail.invalidgeometry (id serial, type varchar(20), geom geometry(MULTIPOLYGON, 2154), PRIMARY KEY(id));

INSERT INTO travail.invalidgeometry (type, geom) VALUES ('Hole Outside Shell', ST_multi(ST_GeomFromText('POLYGON((465000 6700000, 465010 6700000, 465010 6700010, 465000 6700010, 465000 6700000), (465015 6700015, 465015 6700020, 465020 6700020, 465020 6700015, 465015 6700015))',2154)));

INSERT INTO travail.invalidgeometry (type, geom) VALUES ('Nested Holes', ST_multi(ST_GeomFromText('POLYGON((465030 6700000, 465040 6700000, 465040 6700010, 465030 6700010, 465030 6700000), (465032 6700002, 465032 6700008, 465038 6700008, 465038 6700002, 465032 6700002), (465033 6700003, 465033 6700007, 465037 6700007, 465037 6700003, 465033 6700003))',2154)));

INSERT INTO travail.invalidgeometry (type, geom) VALUES ('Dis. Interior', ST_Multi(ST_GeomFromText('POLYGON((465060 6700000, 465070 6700000,465070 6700010, 465060 6700010, 465060 6700000), (465065 6700000, 465070 6700005, 465065 6700010, 465060 6700005, 465065 6700000))', 2154)));

INSERT INTO travail.invalidgeometry (type, geom) VALUES ('Self Intersect.', ST_multi(ST_GeomFromText('POLYGON((465090 6700000, 465100 6700010, 465090 6700010, 465100 6700000, 465090 6700000))',2154)));

INSERT INTO travail.invalidgeometry (type, geom) VALUES ('Ring Self Intersect.', ST_multi(ST_GeomFromText('POLYGON((465125 6700000, 465130 6700000, 465130 6700010, 465120 6700010, 465120 6700000, 465125 6700000, 465123 6700003, 465125 6700006, 465127 6700003, 465125 6700000))',2154)));

INSERT INTO travail.invalidgeometry (type, geom) VALUES ('Nested Shells', ST_multi(ST_GeomFromText('MULTIPOLYGON(((465150 6700000, 465160 6700000, 465160 6700010, 465150 6700010, 465150 6700000)),(( 465152 6700002, 465158 6700002, 465158 6700008, 465152 6700008, 465152 6700002)))',2154)));

Visualiser la table dans QGIS :

Chacun de ces objets est invalide.

Vérifions-le avec la requête suivante :

SELECT id, type, ST_IsValidReason(geom) FROM travail.invalidgeometry WHERE NOT ST_IsValid(geom);

qui nous renvoi :